The Epsilon-Greedy Algorithm

The Epsilon-Greedy algorithm is a cornerstone of reinforcement learning (RL), known for its simplicity and effectiveness in balancing exploration (discovering new information) and exploitation (utilizing existing knowledge). This blog delves into every aspect of the Epsilon-Greedy algorithm, from its conceptual underpinnings to its applications, mathematical formulations, implementation, and practical considerations. By the end, you’ll have a deep understanding of this essential RL algorithm and how to leverage it for real-world problems.

1. The Core Problem: Exploration vs. Exploitation

In reinforcement learning, an agent interacts with an environment to maximize its cumulative reward over time. The agent faces a dilemma:

Exploration: Investigating actions that might lead to higher rewards in the future but may yield lower rewards in the short term.
Exploitation: Selecting actions that maximize immediate rewards based on the agent’s current knowledge.

Balancing these two objectives is critical for efficient learning. If the agent over-explores, it wastes time on suboptimal actions. If it over-exploits, it risks missing better opportunities due to incomplete information.

The Epsilon-Greedy algorithm offers a simple yet effective solution by introducing a probabilistic approach to action selection.

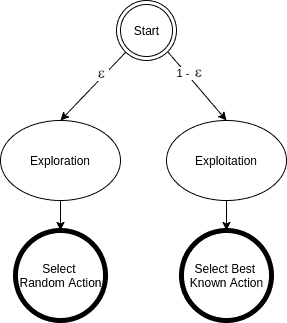
2. What is the Epsilon-Greedy Algorithm?

The Epsilon-Greedy algorithm is a decision-making strategy that allows an agent to balance exploration and exploitation dynamically. It operates as follows:

With probability ϵ\epsilon, the agent explores by selecting a random action.
With probability 1−ϵ1 – \epsilon, the agent exploits by selecting the action with the highest estimated value based on its current knowledge.

3. Algorithm Workflow

Step-by-Step Process

Initialize Values: Start with an initial estimate of action values (Q(a)Q(a)) for each possible action aa, typically set to zero or small random values.
Choose an Action:
- Generate a random number rr between 0 and 1.
- If r<ϵr < \epsilon, select a random action (exploration).
- Otherwise, select the action with the highest estimated value Q(a)Q(a) (exploitation).
Perform the Action: Execute the chosen action in the environment and observe the resulting reward (RR).
Update the Estimate: Update the action-value estimate (Q(a)Q(a)) using an appropriate update rule: Q(a)←Q(a)+α⋅(R−Q(a))Q(a) \leftarrow Q(a) + \alpha \cdot (R – Q(a)) Here, α\alpha is the learning rate, and RR is the observed reward.
Repeat: Continue the process for a predefined number of iterations or until the agent converges to an optimal policy.

4. Mathematical Foundations

The Epsilon-Greedy algorithm is rooted in the concept of action-value estimation. It uses sample-based learning to estimate the value of each action:

Action-Value Function

The action-value function Q(a)Q(a) represents the expected reward for taking action aa. Over time, the agent refines its estimate of Q(a)Q(a) using rewards received from the environment.

Update Rule

The update rule can be written as: Q(a)←Q(a)+1N(a)⋅(R−Q(a))Q(a) \leftarrow Q(a) + \frac{1}{N(a)} \cdot (R – Q(a))

Where:

Q(a)Q(a): Current estimate of the action value.
RR: Reward received for the action.
N(a)N(a): Number of times the action aa has been selected.

Alternatively, a constant learning rate (α\alpha) can be used: Q(a)←Q(a)+α⋅(R−Q(a))Q(a) \leftarrow Q(a) + \alpha \cdot (R – Q(a))

5. Balancing Exploration and Exploitation

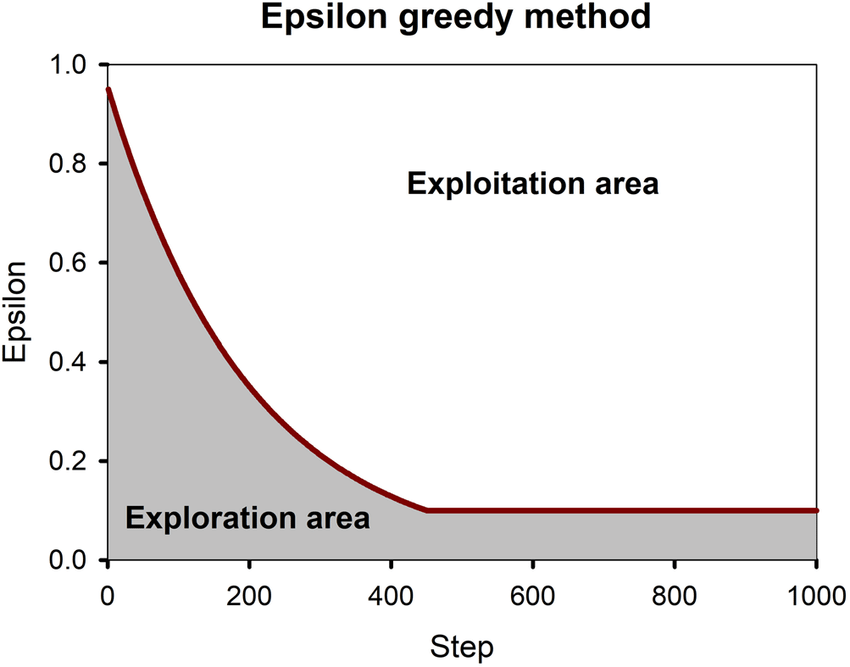
The trade-off between exploration and exploitation is controlled by the parameter ϵ\epsilon. Here’s how different values of ϵ\epsilon affect the agent’s behavior:

High ϵ\epsilon (e.g., 0.9):
- Encourages exploration.
- Useful at the beginning of learning when the agent has little knowledge.
Low ϵ\epsilon (e.g., 0.1):
- Encourages exploitation.
- Suitable for later stages when the agent has accumulated sufficient knowledge.

A popular approach is to use epsilon decay, where ϵ\epsilon starts high and gradually decreases over time. This ensures that the agent explores more in the early stages and exploits as it gains confidence.

Epsilon Decay Formula

ϵ=max⁡(ϵmin,ϵinitial⋅exp⁡(−decay rate⋅t))\epsilon = \max(\epsilon_{\text{min}}, \epsilon_{\text{initial}} \cdot \exp(-\text{decay rate} \cdot t))

Where:

ϵmin\epsilon_{\text{min}}: Minimum value of ϵ\epsilon.
ϵinitial\epsilon_{\text{initial}}: Initial value of ϵ\epsilon.
tt: Current time step.
decay rate\text{decay rate}: Controls the rate of decrease.

6. Practical Applications of Epsilon-Greedy

6.1 Multi-Armed Bandit Problems

Optimizing slot machine payouts.
Allocating resources in online advertising.

6.2 Reinforcement Learning

Training agents in environments like OpenAI Gym.
Learning policies in dynamic, reward-driven tasks.

6.3 Online Recommendation Systems

Personalizing content while testing new items.
Balancing exploration of new movies, songs, or products and exploiting known user preferences.

6.4 Game AI

Balancing aggressive moves (exploitation) with experimental strategies (exploration).

7. Advantages of Epsilon-Greedy

Simplicity: Easy to implement with minimal computational overhead.
Flexibility: Works well with both discrete and continuous action spaces.
Dynamic Behavior: Epsilon decay allows the algorithm to adapt over time.

8. Limitations of Epsilon-Greedy

Random Exploration: Random action selection can lead to inefficient exploration.
Suboptimal in Complex Environments: May not work well when action-value estimates are noisy or rewards are sparse.
Fixed Probability: Requires careful tuning of ϵ\epsilon to achieve a good balance.

9. Enhancements to Epsilon-Greedy

To address its limitations, several variations and enhancements have been proposed:

9.1 Optimistic Initialization

Initialize Q(a)Q(a) to high values to encourage exploration.

9.2 Upper Confidence Bound (UCB)

Use confidence intervals to balance exploration and exploitation:

a=arg⁡max⁡(Q(a)+c⋅ln⁡(t)N(a))a = \arg\max \left( Q(a) + c \cdot \sqrt{\frac{\ln(t)}{N(a)}} \right)

9.3 Contextual Bandits

Extend Epsilon-Greedy to consider context (e.g., user preferences, environmental states).

10. Python Implementation

Below is a Python implementation of the Epsilon-Greedy algorithm for a multi-armed bandit problem:

import numpy as np

# Number of actions (arms)
num_actions = 10
# Number of steps
num_steps = 1000
# Exploration probability (epsilon)
epsilon = 0.1

# Initialize action-value estimates and action counts
Q = np.zeros(num_actions)  # Estimated values for each action
N = np.zeros(num_actions)  # Count of times each action was selected

# Rewards for each action (hidden true values)
true_rewards = np.random.randn(num_actions)

def select_action(Q, epsilon):
    """Epsilon-Greedy Action Selection."""
    if np.random.rand() < epsilon:
        # Explore: Choose a random action
        return np.random.randint(0, num_actions)
    else:
        # Exploit: Choose the action with the highest estimated value
        return np.argmax(Q)

def update_Q(Q, N, action, reward):
    """Update the Q-value estimate for the chosen action."""
    N[action] += 1
    Q[action] += (reward - Q[action]) / N[action]

# Simulation loop
for step in range(num_steps):
    action = select_action(Q, epsilon)
    reward = true_rewards[action] + np.random.randn()  # Add some noise
    update_Q(Q, N, action, reward)

# Display final action-value estimates
print("Estimated Q-values:", Q)
print("True rewards:", true_rewards)

HTML Code Editor Version

To facilitate easy testing, the code is provided in an HTML format for integration with online editors:

<!DOCTYPE html>
<html>
<head>
    <title>Epsilon-Greedy Algorithm</title>
</head>
<body>
    <h1>Epsilon-Greedy Algorithm in Python</h1>
    <pre>
<code>
import numpy as np

# Number of actions (arms)
num_actions = 10
# Number of steps
num_steps = 1000
# Exploration probability (epsilon)
epsilon = 0.1

# Initialize action-value estimates and action counts
Q = np.zeros(num_actions)  # Estimated values for each action
N = np.zeros(num_actions)  # Count of times each action was selected

# Rewards for each action (hidden true values)
true_rewards = np.random.randn(num_actions)

def select_action(Q, epsilon):
    """Epsilon-Greedy Action Selection."""

if np.random.rand() < epsilon: # Explore: Choose a random action return np.random.randint(0, num_actions) else: # Exploit: Choose the action with the highest estimated value return np.argmax(Q)

def update_Q(Q, N, action, reward): “””Update the Q-value estimate for the chosen action.””” N[action] += 1 Q[action] += (reward – Q[action]) / N[action]

Simulation loop

for step in range(num_steps): action = select_action(Q, epsilon) reward = true_rewards[action] + np.random.randn() # Add some noise update_Q(Q, N, action, reward)

Display final action-value estimates

print(“Estimated Q-values:”, Q) print(“True rewards:”, true_rewards)

11. Conclusion

The Epsilon-Greedy algorithm is a foundational tool in reinforcement learning, providing a simple yet effective method for balancing exploration and exploitation. Its widespread use across diverse applications, from online recommendations to game AI, demonstrates its versatility. By understanding its principles, tuning its parameters, and extending its capabilities, you can harness its full potential for solving real-world problems.

The Epsilon-Greedy Algorithm: A Comprehensive Guide 2024