Multi-Armed Bandit Problem Solved Using UCB Algorithm: COMPREHENSIVE GUIDE 2024

Multi-Armed Bandit Problem Solved Using UCB Algorithm

http://Multi-Armed Bandit Problem Solved Using UCB Algorithm

The Multi-Armed Bandit (MAB) problem is a foundational concept in reinforcement learning and decision theory, frequently encountered in scenarios requiring a balance between exploration and exploitation. This blog post delves deeply into the MAB problem, its significance, the UCB (Upper Confidence Bound) algorithm as a solution, and a Python implementation with thorough explanations. By the end of this blog, you’ll have a comprehensive understanding of solving the MAB problem using UCB, supplemented with code formatted for easy integration into web platforms.

Introduction to Multi-Armed Bandit Problem

What is the Multi-Armed Bandit Problem?

The Multi-Armed Bandit (MAB) problem derives its name from the one-armed bandit (slot machines). Imagine standing in front of multiple slot machines, each with an unknown probability of giving a reward. Your task is to maximize your earnings by deciding which machines to play, how many times to play each machine, and in what sequence. However, you face a trade-off:

Exploration: Testing different machines to gather information about their reward probabilities.
Exploitation: Playing the machine you believe will yield the highest reward based on the information you have.

Applications of the MAB Problem

The MAB problem extends beyond slot machines and finds applications in various fields:

Online Advertising: Selecting the most effective ad for users.
Clinical Trials: Choosing the best treatment dynamically based on ongoing patient responses.
Product Recommendations: Displaying products with the highest likelihood of purchase.
A/B Testing: Dynamically allocating more traffic to better-performing versions of a webpage or product.

Upper Confidence Bound (UCB) Algorithm

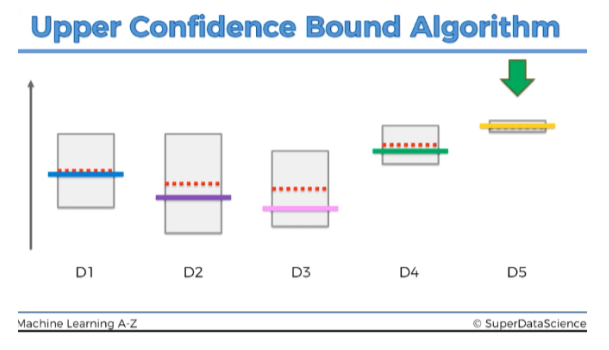
What is UCB?

The UCB algorithm provides a mathematical framework for balancing exploration and exploitation. It assigns an “upper confidence bound” to each arm, which is calculated based on two factors:

The average reward obtained from the arm so far (exploitation).
A confidence term that decreases as the arm is pulled more frequently (exploration).

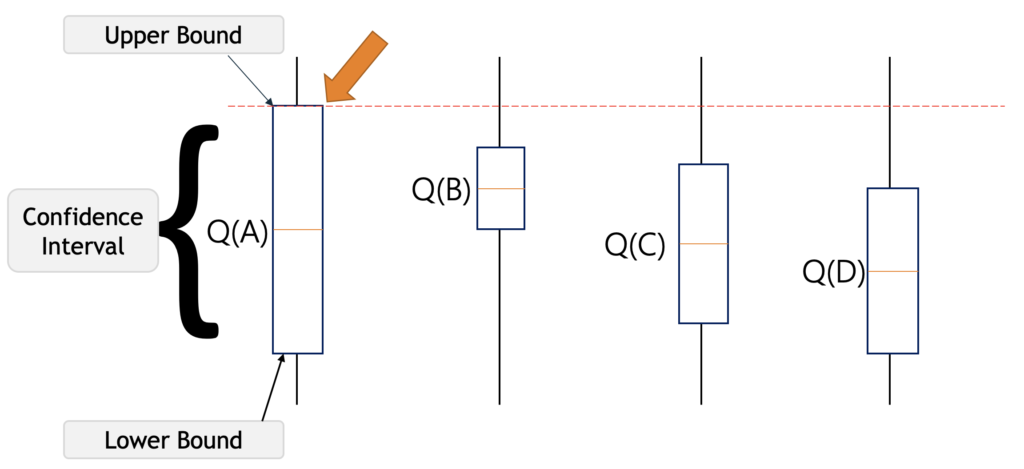
The UCB Formula

The UCB value for an arm jj at time step tt is computed as: UCBj=Xˉj+2ln⁡tnjUCB_{j} = \bar{X}_{j} + \sqrt{\frac{2 \ln t}{n_{j}}}

Where:

Xˉj\bar{X}_{j}: Average reward of arm jj (exploitation term).
tt: Current time step (total number of pulls).
njn_{j}: Number of times arm jj has been pulled (exploration term).

The algorithm selects the arm with the highest UCBjUCB_{j} value at each time step.

Intuition Behind UCB

Arms that have been pulled less frequently have a larger confidence term, encouraging exploration.
As more pulls occur, the confidence term reduces, focusing more on exploitation of high-reward arms.

Python Implementation of UCB

Below is a Python implementation of the UCB algorithm for solving the Multi-Armed Bandit problem. The code is provided in HTML format for easy embedding into a website or blog.

<!DOCTYPE html>
<html>
<head>
    <title>UCB Algorithm for Multi-Armed Bandit</title>
</head>
<body>
    <h2>Python Code for UCB Algorithm</h2>
    <pre>
        <code>
import numpy as np
import matplotlib.pyplot as plt

# Number of arms and iterations
n_arms = 5
n_iterations = 1000

# Simulated rewards for each arm (true probabilities of rewards)
true_rewards = [0.1, 0.5, 0.8, 0.3, 0.6]

# Variables to track rewards and pulls
rewards = [0] * n_arms
pulls = [0] * n_arms
total_reward = 0

# UCB Algorithm
for t in range(1, n_iterations + 1):
    arm_selected = 0
    max_upper_bound = 0

    for i in range(n_arms):
        if pulls[i] > 0:
            avg_reward = rewards[i] / pulls[i]
            confidence = np.sqrt(2 * np.log(t) / pulls[i])
            upper_bound = avg_reward + confidence
        else:
            upper_bound = 1e400  # Infinite value for unpulled arms

        if upper_bound > max_upper_bound:
            max_upper_bound = upper_bound
            arm_selected = i

    # Simulate reward for the selected arm
    reward = np.random.binomial(1, true_rewards[arm_selected])
    rewards[arm_selected] += reward
    pulls[arm_selected] += 1
    total_reward += reward

# Display results
print("Number of times each arm was pulled:")
for i in range(n_arms):
    print(f"Arm {i + 1}: {pulls[i]} times")

print(f"\nTotal Reward: {total_reward}")

# Visualization
plt.bar(range(n_arms), pulls, color='blue', alpha=0.7)
plt.xlabel('Arms')
plt.ylabel('Number of Pulls')
plt.title('Number of Times Each Arm was Pulled')
plt.show()
        </code>
    </pre>
</body>
</html>

Explanation of the Code

Setup:
- n_arms defines the number of slot machines.
- n_iterations sets the total number of pulls (time steps).
- true_rewards represents the actual reward probabilities for each arm.
Tracking Variables:
- rewards: Tracks cumulative rewards obtained from each arm.
- pulls: Tracks the number of times each arm is played.
UCB Calculation:
- For each time step, the UCB value is computed for every arm.
- The arm with the highest UCB value is selected.
Simulation of Rewards:
- Rewards are generated using the np.random.binomial function, which simulates success/failure based on the true probability of the selected arm.
Output:
- The number of times each arm was pulled.
- The total reward obtained.
Visualization:
- A bar chart shows the number of times each arm was pulled, highlighting the algorithm’s ability to favor higher-reward arms.

Insights from Results

Exploration Phase:
- Initially, the algorithm explores all arms to estimate their average rewards.
Exploitation Phase:
- Over time, the algorithm focuses more on the arms with higher average rewards.
Minimizing Regret:
- The UCB algorithm minimizes regret by gradually converging to the optimal arm.

Advantages of UCB Algorithm

Simple and Efficient:
- Easy to implement with minimal computational overhead.
Theoretical Guarantees:
- The algorithm has proven guarantees for minimizing regret over time.
Adaptability:
- Works well in non-stationary environments with slight modifications.

Applications of UCB in Real-World Scenarios

E-commerce:
- Dynamically displaying products with higher purchase probabilities.
Digital Marketing:
- Optimizing ad placement and user targeting.
Clinical Research:
- Adjusting treatment assignments dynamically based on patient outcomes.
Gaming:
- Balancing difficulty levels or resource allocations in real-time.

Challenges and Considerations

Cold Start Problem:
- During the initial exploration phase, the algorithm may pull suboptimal arms.
Scalability:
- In scenarios with a very high number of arms, computation can become intensive.
Non-Stationarity:
- If reward probabilities change over time, the algorithm may require re-tuning or restarting.

Enhancing UCB for Complex Scenarios

Contextual Bandits:
- Incorporating additional contextual information (e.g., user preferences) to improve decision-making.
Dynamic Environments:
- Adjusting the confidence term to adapt to changing reward distributions.
Hybrid Models:
- Combining UCB with other algorithms like Thompson Sampling for improved performance.

Conclusion

The UCB algorithm provides an elegant and effective solution to the Multi-Armed Bandit problem. Its ability to balance exploration and exploitation makes it widely applicable across industries. The Python implementation above offers a practical demonstration of the algorithm in action.

Use the code to experiment with different reward probabilities and explore how the UCB algorithm performs in various scenarios. Happy learning!