Solving a Maze Using Q-Learning: A Practical Guide to Implementing Reinforcement Learning
http://Solving a Maze Using Q-Learning: A Practical Guide to Implementing Reinforcement Learning
Reinforcement Learning (RL) is a branch of machine learning where agents learn to make decisions by interacting with an environment, receiving feedback in the form of rewards or penalties, and using that feedback to improve their actions. One of the classic problems used to demonstrate RL algorithms is a maze navigation task, where an agent must navigate a maze to reach a goal while maximizing the accumulated rewards. In this blog, we will dive into how we can solve such a task using Q-Learning, a model-free reinforcement learning algorithm. We will cover the theoretical background, followed by a step-by-step implementation of the algorithm to navigate a maze and maximize the rewards.
What is Q-Learning?
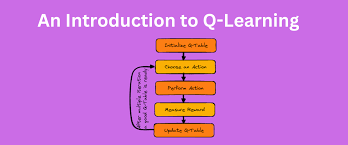
Q-Learning is a model-free reinforcement learning algorithm that helps an agent learn how to act optimally in an environment by updating a value function known as the Q-function (short for quality function). The Q-function, Q(s,a)Q(s, a), represents the expected future reward for taking action aa in state ss, and following the optimal policy thereafter.
Q-learning uses an off-policy approach, meaning it learns the value of the optimal policy independently of the agent’s current actions. The key update rule in Q-learning is: Q(st,at)←Q(st,at)+α[Rt+1+γmaxa′Q(st+1,a′)−Q(st,at)]Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ R_{t+1} + \gamma \max_{a’} Q(s_{t+1}, a’) – Q(s_t, a_t) \right]
Where:
- sts_t is the current state,
- ata_t is the action taken,
- Rt+1R_{t+1} is the reward received for taking action ata_t,
- γ\gamma is the discount factor, which controls how much future rewards are valued compared to immediate rewards,
- α\alpha is the learning rate, which controls how much new information overrides old information.
The goal of Q-learning is to learn the optimal Q-function, from which the agent can derive an optimal policy — the best action to take in each state.
Problem Setup: Maze Navigation
For this practical task, imagine we have a maze environment where the agent starts at a specific location and needs to reach a goal while avoiding obstacles. The agent receives rewards for reaching the goal and penalties for hitting walls or obstacles. Our goal is to implement Q-Learning to help the agent learn the optimal path from start to goal.
Components of the Maze:
- States: Each position in the maze is a state. For example, if we have a grid maze of size 5×5, there are 25 states, each representing a unique position in the grid.
- Actions: The possible actions at each state are the movements the agent can make. Typically, these are:
- Up
- Down
- Left
- Right
- Rewards: The agent receives a positive reward when it reaches the goal and a negative reward for hitting obstacles or walls. States leading to the goal have a positive reward (e.g., +10), and states with walls or obstacles have a negative reward (e.g., -1).
- Transitions: The transition from one state to another depends on the agent’s actions. If the agent attempts to move into a wall, it remains in the same state.
Q-Learning Algorithm to Solve the Maze
We will now implement the Q-Learning algorithm to solve the maze navigation problem. Let’s break the implementation into the following steps:
Step 1: Define the Maze Environment
First, we need to define the maze grid and the corresponding rewards. The maze will be represented as a grid, with each cell in the grid representing a state. Some cells will be walls, some will be open spaces, and one will be the goal.
Step 2: Initialize Q-table
The Q-table stores the Q-values for each state-action pair. Initially, all Q-values are set to zero. Over time, these values will be updated using the Q-learning update rule.
Step 3: Define the Q-Learning Update Rule
The Q-learning update rule will update the Q-values based on the agent’s interactions with the environment.
Step 4: Implement the Exploration and Exploitation Strategy
To balance exploration (trying new actions) and exploitation (choosing the best-known action), we use an epsilon-greedy policy. In this policy:
- With probability ϵ\epsilon, the agent explores a random action.
- With probability 1−ϵ1 – \epsilon, the agent exploits the best-known action based on the Q-values.
Step 5: Train the Agent
The agent will interact with the maze environment, taking actions, receiving rewards, and updating its Q-table using the Q-learning update rule. Over time, it will learn the optimal policy to navigate the maze.
Q-Learning Implementation in Python

Below is a Python implementation of the Q-learning algorithm for a simple maze navigation task.
import numpy as np
import random
# Define the Maze Environment (5x5 grid)
class MazeEnv:
def __init__(self):
# Create a 5x5 grid, where 1 represents a wall, 0 is an open space, and 9 is the goal
self.maze = np.zeros((5, 5))
self.maze[1, 1] = 1 # Wall
self.maze[1, 2] = 1 # Wall
self.maze[1, 3] = 1 # Wall
self.maze[3, 1] = 1 # Wall
self.maze[3, 3] = 1 # Wall
self.maze[4, 4] = 9 # Goal
self.start = (0, 0) # Starting position
self.current_state = self.start
def reset(self):
self.current_state = self.start
return self.current_state
def step(self, action):
# Define possible actions: 0 = Up, 1 = Down, 2 = Left, 3 = Right
x, y = self.current_state
if action == 0: # Up
if x > 0 and self.maze[x - 1, y] != 1:
x -= 1
elif action == 1: # Down
if x < 4 and self.maze[x + 1, y] != 1:
x += 1
elif action == 2: # Left
if y > 0 and self.maze[x, y - 1] != 1:
y -= 1
elif action == 3: # Right
if y < 4 and self.maze[x, y + 1] != 1:
y += 1
self.current_state = (x, y)
# Check if goal is reached
if self.maze[x, y] == 9:
return self.current_state, 10, True # Reward 10 for reaching the goal
elif self.maze[x, y] == 1:
return self.current_state, -1, False # Penalty for hitting a wall
else:
return self.current_state, -0.1, False # Small penalty for moving
# Q-Learning Agent
class QLearningAgent:
def __init__(self, env, alpha=0.1, gamma=0.9, epsilon=0.1):
self.env = env
self.alpha = alpha # Learning rate
self.gamma = gamma # Discount factor
self.epsilon = epsilon # Exploration factor
self.q_table = np.zeros((5, 5, 4)) # Q-table for each state-action pair (5x5 grid, 4 actions)
def choose_action(self, state):
if random.uniform(0, 1) < self.epsilon:
return random.randint(0, 3) # Explore
else:
x, y = state
return np.argmax(self.q_table[x, y]) # Exploit
def update_q_value(self, state, action, reward, next_state):
x, y = state
next_x, next_y = next_state
max_q_next = np.max(self.q_table[next_x, next_y]) # Max Q-value for next state
self.q_table[x, y, action] = self.q_table[x, y, action] + self.alpha * (reward + self.gamma * max_q_next - self.q_table[x, y, action])
# Main Training Loop
env = MazeEnv()
agent = QLearningAgent(env)
episodes = 1000 # Number of episodes for training
for episode in range(episodes):
state = env.reset()
done = False
while not done:
action = agent.choose_action(state)
next_state, reward, done = env.step(action)
agent.update_q_value(state, action, reward, next_state)
state = next_state
if episode % 100 == 0:
print(f"Episode {episode} complete.")
# After training, print the learned Q-table
print("Learned Q-table:")
print(agent.q_table)
Explanation of the Code:
- MazeEnv Class: This class represents the maze environment. It defines the maze structure, where 1’s represent walls, 0’s represent open spaces, and 9 represents the
goal. The step method handles the movement based on the agent’s action, and returns the next state, reward, and whether the goal has been reached.
- QLearningAgent Class: This class implements the Q-learning agent. It has a Q-table, which is a 3D NumPy array with dimensions 5×5×45 \times 5 \times 4 (for each of the 5×5 grid states and 4 possible actions). The
choose_actionmethod implements the epsilon-greedy policy, and theupdate_q_valuemethod updates the Q-values using the Q-learning update rule. - Training Loop: The agent is trained over 1000 episodes. In each episode, the agent starts from the initial position, takes actions, and updates the Q-values based on the feedback from the environment.
Conclusion
Q-Learning is a powerful reinforcement learning algorithm that can solve problems like maze navigation, where an agent needs to learn an optimal policy through trial and error. In this blog, we implemented Q-Learning to navigate a simple 5×5 maze, where the agent learns to avoid walls and reach the goal efficiently. By updating the Q-values using the Q-learning algorithm, the agent improves its decision-making and finds the optimal path to maximize its cumulative rewards.
This basic implementation can be expanded to handle more complex environments, continuous state spaces, or more advanced function approximation techniques like neural networks for large state-action spaces.