comprehensive guide Regularization Techniques in Deep Neural Networks 2024

Introduction

Regularization is a crucial technique in Deep Neural Networks (DNNs) to improve generalization and prevent overfitting. When models are too complex, they tend to memorize training data rather than learning generalizable patterns.

🚀 Why is Regularization Important?

✔ Prevents overfitting and improves model performance on unseen data
✔ Reduces complexity while maintaining accuracy
✔ Ensures stable training and better convergence

Topics Covered:

✅ Generalization in DNNs
✅ Overfitting vs. Underfitting
✅ L1 and L2 Regularization
✅ Dropout Regularization
✅ Batch Normalization

1. Generalization in Deep Learning

The primary goal of a machine learning model is to generalize well. Generalization refers to a model’s ability to perform well on new, unseen data.

🔹 Key Factors Affecting Generalization: ✔ Model Complexity – Complex models with too many parameters tend to overfit.
✔ Training Data Size – Small datasets increase the risk of memorization rather than learning patterns.
✔ Regularization Techniques – Reduce unnecessary complexity and prevent overfitting.

🚀 Example: Image Recognition

A model trained on 10,000 dog images should recognize new dog images without memorizing training samples.

✅ Generalization is the balance between underfitting and overfitting.

2. Overfitting vs. Underfitting

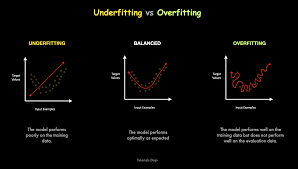
A well-trained model should have low training error and low validation error.

Scenario	Training Accuracy	Validation Accuracy	Issue
Underfitting	Low	Low	Model is too simple
Overfitting	High	Low	Model memorizes training data
Good Model	High	High	Well-generalized

🚀 Example: Predicting House Prices ✔ Underfitting: The model predicts all houses have the same price.
✔ Overfitting: The model memorizes each house but fails on new data.

✅ Goal: Achieve high training and validation accuracy without overfitting.

3. L1 and L2 Regularization (Weight Decay)

L1 and L2 regularization techniques add a penalty to large weights, forcing the model to be simpler and more generalizable.

✅ L1 Regularization (Lasso)

🔹 Encourages sparsity by setting some weights to zero
🔹 Useful for feature selection
🔹 Formula:LL1=λ∑∣w∣L_{L1} = \lambda \sum |w| LL1=λ∑∣w∣

🚀 Example: Feature Selection in NLP

L1 regularization automatically removes less useful words, improving performance.

✅ L1 is ideal for models needing feature reduction.

✅ L2 Regularization (Ridge Regression)

🔹 Penalizes large weights but does not force them to zero
🔹 Encourages smooth, small weight values
🔹 Formula:LL2=λ∑w2L_{L2} = \lambda \sum w^2 LL2=λ∑w2

🚀 Example: Deep Neural Networks

L2 regularization prevents a few neurons from dominating the learning process.

✅ L2 is preferred in deep networks to stabilize learning.

4. Dropout Regularization

Dropout is a simple but powerful regularization technique that randomly drops neurons during training.

🔹 How Dropout Works: ✔ During training, neurons are randomly turned off with probability p.
✔ Prevents co-dependency among neurons.
✔ Forces the model to learn distributed representations.

🚀 Example: Improving CNN Performance

A CNN trained on handwritten digits with dropout (p=0.5) performs better on unseen digits.

✅ Dropout reduces overfitting and improves model robustness.

5. Early Stopping

Early stopping halts training when validation error starts increasing, preventing overfitting.

🔹 Steps to Apply Early Stopping: ✔ Monitor validation loss during training.
✔ Stop training when the validation loss stops improving.
✔ Use the best weights from the lowest validation loss.

🚀 Example: Training a DNN for Sentiment Analysis

Training for too long memorizes training tweets instead of learning sentiment.

✅ Early stopping ensures efficient training and prevents unnecessary computations.

6. Vanishing and Exploding Gradients

Deep networks suffer from unstable gradients that can slow or prevent learning.

Issue	Impact	Solution
Vanishing Gradient	Gradients shrink to near zero	Use ReLU activation instead of Sigmoid
Exploding Gradient	Gradients grow exponentially	Use Gradient Clipping

🚀 Example: Deep Recurrent Networks

RNNs suffer from vanishing gradients, making it difficult to remember long-term dependencies.

✅ Use batch normalization and proper weight initialization to stabilize gradients.

7. Batch Normalization (BatchNorm)

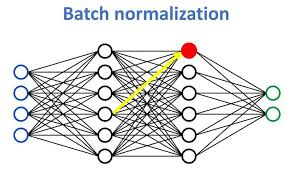
Batch Normalization normalizes activations across mini-batches, making training faster and more stable.

🔹 Why Use Batch Normalization? ✔ Reduces internal covariate shift (i.e., distribution changes during training).
✔ Allows higher learning rates, improving convergence speed.
✔ Acts as a form of regularization, reducing the need for dropout.

🚀 Example: Faster Training for CNNs

A CNN with batch normalization trains 2x faster than without it.

✅ BatchNorm is widely used in deep learning for speed and stability.

8. Best Practices for Regularization

✔ Use L2 regularization for smooth weight distribution.
✔ Apply dropout (p = 0.5) to prevent neuron over-reliance.
✔ Use early stopping to prevent excessive training.
✔ Normalize input features to stabilize gradients.
✔ Use batch normalization to improve convergence.

🚀 Example: Regularizing a Deep Learning Model

Combining dropout + batch normalization + L2 regularization ensures robust, generalizable models.

✅ Regularization is essential for training stable deep networks.

9. Conclusion

Regularization improves deep learning models by reducing overfitting and enhancing generalization.

✅ Key Takeaways

✔ L1 (Lasso) selects important features, while L2 (Ridge) prevents large weights.
✔ Dropout randomly disables neurons to improve generalization.
✔ Early stopping prevents unnecessary training.
✔ Batch normalization speeds up training and stabilizes gradients.

💡 Which regularization techniques do you use in your models? Let’s discuss in the comments! 🚀

Would you like a step-by-step Python tutorial on implementing dropout and batch normalization? 😊