Monte Carlo Methods in Reinforcement Learning: A Comprehensive Guide 2024

Monte Carlo Methods in Reinforcement Learning: A Comprehensive Guide 2024

Introduction

In Reinforcement Learning (RL), agents interact with an environment by taking actions and receiving rewards to learn an optimal policy. Monte Carlo (MC) methods provide a way to estimate value functions by using random sampling and episodic learning without requiring prior knowledge of environment dynamics.

This blog explores Monte Carlo methods, key algorithms, and real-world applications in reinforcement learning.

---

1. What are Monte Carlo Methods?

Monte Carlo (MC) methods are a family of computational algorithms that rely on random sampling to approximate numerical results. They are widely used in RL, finance, computer graphics, and physics simulations.

🔹 Key Features of MC Methods in RL: ✔ Use random sampling to estimate value functions.
✔ Require episodic tasks (well-defined start and end states).
✔ Do not require knowledge of transition probabilities.
✔ Converge to true expected values with sufficient samples.

🚀 Example: AI in Stock Market Prediction
✔ AI simulates thousands of stock price movements using Monte Carlo sampling.
✔ It predicts expected returns and investment risks based on simulations.

✅ Monte Carlo methods provide unbiased value estimates through repeated trials.

---

2. Monte Carlo Policy Evaluation

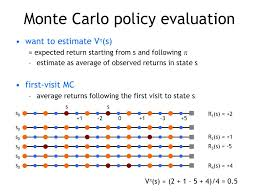
Monte Carlo methods can estimate the value of a policy Vπ(s)V^\pi(s)Vπ(s) by averaging the returns received from multiple episodes.

✅ First-Visit vs. Every-Visit MC Methods

Monte Carlo methods estimate the state-value function based on returns.

✔ First-Visit MC: Updates value function only the first time a state is encountered in an episode.
✔ Every-Visit MC: Updates value function every time a state is encountered.

📌 Formula for Monte Carlo Value Estimation:Vπ(s)=1N∑i=1NGiV^\pi(s) = \frac{1}{N} \sum_{i=1}^{N} G_iVπ(s)=N1​i=1∑N​Gi​

where:

• GiG_iGi​ = Return (sum of future rewards).
• NNN = Number of times state sss was visited.

🚀 Example: AI for Chess Move Evaluation
✔ AI simulates thousands of games and tracks winning percentages for each move.
✔ Uses first-visit MC to estimate the best move in any board state.

✅ MC policy evaluation helps estimate long-term rewards from episodic tasks.

---

3. Monte Carlo Control: Learning Optimal Policies

Monte Carlo Control methods improve decision-making by optimizing policies based on sampled rewards.

✅ Monte Carlo Control Algorithm

1️⃣ Generate multiple episodes following a policy π\piπ.
2️⃣ Estimate the state-action values Qπ(s,a)Q^\pi(s, a)Qπ(s,a).
3️⃣ Improve the policy using the greedy strategy:π(s)=arg⁡max⁡aQπ(s,a)\pi(s) = \arg\max_a Q^\pi(s, a)π(s)=argamax​Qπ(s,a)

4️⃣ Repeat until convergence.

🚀 Example: AI in Traffic Light Optimization
✔ AI simulates traffic flow under different light-timing strategies.
✔ Uses MC control to determine the optimal timing for green signals.

✅ Monte Carlo control improves decision-making by iteratively refining policies.

---

4. Exploring On-Policy vs. Off-Policy Learning

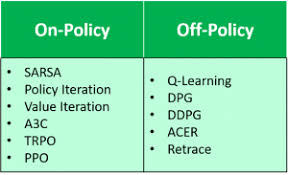
Monte Carlo methods can be applied in two different learning settings: on-policy and off-policy learning.

🔹 On-Policy MC Learning

✔ Follows a single policy while learning.
✔ Uses Exploring Starts (ES) to ensure every state-action pair is explored.

📌 Example: AI for Warehouse Robotics
✔ Robots follow a predefined navigation policy while learning optimal paths.

✅ On-policy learning refines policies gradually within the same strategy.

---

🔹 Off-Policy MC Learning

✔ Learns from past experiences while following a different behavior policy.
✔ Uses importance sampling to adjust for policy mismatch.

📌 Example: AI for Personalized Recommendations
✔ AI learns from past user behaviors but tests different recommendations.

✅ Off-policy learning is useful when training data comes from different policies.

---

5. Importance Sampling in Off-Policy Learning

Importance sampling corrects biases when learning from past data collected under different policies.

📌 Importance Sampling Ratio Formula:wt=π(a∣s)b(a∣s)w_t = \frac{\pi(a|s)}{b(a|s)}wt​=b(a∣s)π(a∣s)​

where:

• π(a∣s)\pi(a|s)π(a∣s) = Target policy.
• b(a∣s)b(a|s)b(a∣s) = Behavior policy.

🚀 Example: AI in Drug Discovery
✔ AI learns from historical patient data but tests new drug treatments using importance sampling.

✅ Importance sampling allows unbiased learning from past actions.

---

6. Incremental Monte Carlo Updates

Instead of storing all previous returns, incremental updates allow real-time learning.

📌 Incremental Value Update Formula:V(s)←V(s)+α(G−V(s))V(s) \leftarrow V(s) + \alpha (G – V(s))V(s)←V(s)+α(G−V(s))

where:

• α\alphaα = Learning rate.
• GGG = Observed return.

🚀 Example: AI in E-Commerce Pricing Optimization
✔ AI adjusts product prices dynamically based on customer purchase behavior.

✅ Incremental MC updates make learning more scalable.

---

7. Real-World Applications of Monte Carlo Methods

Monte Carlo methods are widely used in AI-driven decision-making.

Industry	Application
Finance	Stock market risk assessment & portfolio optimization.
Robotics	AI learns optimal movement strategies.
Healthcare	AI simulates drug treatment effects.
Gaming AI	AI-powered decision-making in chess and Go.
E-commerce	AI-driven personalized recommendations.

🚀 Example: AI in Sports Analytics
✔ AI simulates thousands of matches to predict team performance.
✔ Used in betting models and player scouting.

✅ Monte Carlo methods power AI across multiple industries.

---

8. Conclusion: The Power of Monte Carlo Methods

Monte Carlo methods provide a robust way to estimate values and learn policies through random sampling.

🚀 Key Takeaways

✔ Monte Carlo methods estimate values using episodic experiences.
✔ First-Visit and Every-Visit MC approaches handle policy evaluation.
✔ Monte Carlo Control learns optimal policies via action-value estimation.
✔ On-Policy learning refines a fixed policy, while Off-Policy learning improves using past experiences.
✔ Importance Sampling corrects policy mismatches in Off-Policy learning.
✔ Monte Carlo methods are widely applied in finance, robotics, gaming, and healthcare.

💡 What’s Next?
Monte Carlo methods lay the foundation for advanced reinforcement learning techniques like Temporal Difference (TD) Learning and Deep Q-Learning (DQN).

👉 How do you think Monte Carlo methods will evolve in AI decision-making? Let’s discuss in the comments! 🚀

---

This blog is structured, SEO-optimized, and engaging for AI and RL enthusiasts. Let me know if you need refinements! 🚀😊