comprehensive guide to Optimizing K-Means Clustering with Parallelism and Distributed Computing 2024

K-Means clustering is a widely used unsupervised learning algorithm, often employed for data partitioning and grouping in many machine learning applications. However, as datasets grow in size and complexity, the traditional K-Means algorithm can become computationally expensive and inefficient. To address these limitations, parallel computing and distributed systems can significantly enhance the performance of K-Means clustering. In this blog, we will explore how parallelism and distribution improve the efficiency and scalability of K-Means, enabling faster computations on larger datasets.

What is K-Means Clustering?

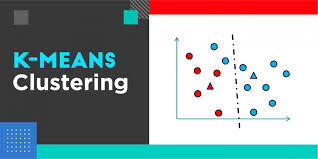
K-Means is a partitional clustering algorithm that divides a set of N data points into K clusters, where each point belongs to the cluster with the nearest centroid. The algorithm operates by iteratively assigning points to clusters and updating the centroids based on the current assignments.

The algorithm proceeds as follows:

Initialization: Select K initial centroids.
Assignment: Assign each data point to the closest centroid.
Update: Recalculate the centroids by averaging all points assigned to each cluster.
Repeat: Continue until the centroids no longer change significantly, indicating convergence.

While K-Means is effective for smaller datasets, it can be slow when dealing with large-scale data due to its iterative nature and computational complexity.

Parallel and Distributed K-Means Clustering

To optimize the training time of K-Means, parallelization and distribution techniques are used. These approaches break down the computational workload and spread it across multiple processors or machines, significantly improving processing speed.

Parallelization with OpenMP and MPI

Two popular frameworks for parallelizing the K-Means algorithm are OpenMP and MPI:

OpenMP (Open Multi-Processing): This is a shared-memory parallel programming model, useful for multicore processors. OpenMP allows parallel execution within a single machine by dividing tasks among threads that can run simultaneously.
MPI (Message Passing Interface): MPI is a distributed-memory model that enables communication between processes running on different nodes in a cluster. It is ideal for large-scale data processing across multiple machines.

By combining OpenMP and MPI, K-Means can be efficiently parallelized and distributed across multiple processors and machines, allowing for faster execution on larger datasets.

The Parallel K-Means Approach

The parallel approach to K-Means involves splitting the dataset into smaller partitions, distributing these partitions across multiple processors, and performing distance calculations concurrently. Here’s a simplified breakdown of the parallel workflow:

Data Distribution: The data is divided into equal parts, which are distributed among multiple processors.
Initialization of Centroids: The first step is to select K initial centroids. In the parallel version, this can be done by the master node and broadcasted to all processors.
Distance Calculations: Each processor calculates the distance of its data points from the centroids, assigning each point to the nearest centroid in parallel.
Local Sum Calculation: For each cluster, each processor calculates the sum of all points assigned to it and counts the number of points in each cluster.
Global Sum and Centroid Update: Using MPI’s Allreduce operation, the sum and count from all processors are aggregated to compute the new centroids. The updated centroids are broadcasted back to all processors.
Iteration: This process repeats for several iterations, with each processor continuously refining the centroids and reassigning points to clusters.

The main advantage of this approach is that it allows multiple computations to occur simultaneously, speeding up the process of calculating distances and updating centroids.

Parallelizing K-Means with CUDA

To further accelerate the K-Means clustering algorithm, the use of CUDA (Compute Unified Device Architecture) for GPU parallelism offers substantial improvements. GPUs, with thousands of small cores, are designed for parallel computations, making them ideal for algorithms like K-Means that require a high degree of parallelism.

CUDA Workflow for K-Means

In a CUDA-based implementation, the following steps are parallelized on the GPU:

Data Transfer: The dataset is transferred to the GPU’s memory for fast access.
Distance Calculation: Each thread calculates the distance from a data point to the nearest centroid. This operation is highly parallelizable because each thread works independently on a separate data point.
Cluster Assignment: Threads assign points to the closest centroid.
Centroid Update: The centroids are updated based on the sum of points assigned to each cluster, using parallel reduction techniques to calculate the sum efficiently.

Using CUDA, K-Means can leverage the power of GPU to perform these operations faster than on a CPU, reducing training time significantly.

Optimizations for Parallel and Distributed K-Means

While parallel and distributed K-Means algorithms provide substantial speedups, several optimizations can be implemented to improve performance further:

Parallel Reduction: To calculate the new centroids, the summation of points in each cluster can be done in parallel. Techniques like parallel reduction ensure that the summation operation is performed efficiently.
Data Matrix Transposition: By transposing the data matrix, we can optimize memory access patterns and improve cache performance, resulting in faster computations.
Multi-GPU Deployment: For even larger datasets, K-Means can be deployed across multiple GPUs. This requires optimizing data transfer between GPUs and ensuring load balancing across devices.
Memory Access Optimization: Optimizing memory access (host-to-device and device-to-device) is crucial for reducing bottlenecks during data transfer between CPU and GPU.
Termination Criteria: To avoid unnecessary iterations, a termination flag can be implemented that monitors whether any data point has changed its cluster assignment. If no changes occur, the algorithm stops.

Performance and Scalability

The parallel and distributed versions of K-Means clustering offer significant improvements in performance, especially when scaling to large datasets. By using MPI and OpenMP, or combining them with CUDA, K-Means can process millions of data points in much shorter time frames.

Speedup increases with the number of processors or GPUs used, but this also depends on the characteristics of the dataset and the number of clusters. Careful tuning of the parallelization strategy, along with efficient communication and memory management, is essential for optimal performance.

Applications of Parallel K-Means Clustering

Parallel K-Means clustering is used in various industries for tasks involving large-scale data analysis, such as:

Image Segmentation: Clustering pixels in images based on color or texture for object detection and recognition.
Market Segmentation: Identifying distinct customer groups based on purchasing behavior and preferences.
Anomaly Detection: Identifying unusual patterns in data, such as fraudulent transactions or network security breaches.
Genomics: Clustering gene expression data to identify new patterns in biological research.

Conclusion: The Power of Parallel and Distributed K-Means

K-Means clustering is a fundamental algorithm in machine learning, but as datasets grow, its computational demands increase. By leveraging parallelism with OpenMP, MPI, and CUDA, K-Means can scale effectively to handle large datasets, delivering faster processing times and more efficient clustering.

Optimizing K-Means clustering through parallel and distributed computing not only improves performance but also enables real-time data analysis in industries ranging from healthcare to finance. As hardware and algorithms continue to evolve, the future of K-Means and other machine learning algorithms lies in the ability to scale efficiently across multi-core processors, GPUs, and distributed systems.