An comprehensive Guide to Bayesian Optimization for Hyperparameter Tuning in Machine Learning 2024

An comprehensive Guide to Bayesian Optimization for Hyperparameter Tuning in Machine Learning 2024

Machine learning (ML) models have become more complex, with hyperparameters playing a critical role in determining their performance. Choosing the right set of hyperparameters can be the difference between an average and an exceptional model. Traditionally, hyperparameter tuning has relied on methods like Grid Search and Random Search, but these techniques are often inefficient, requiring vast amounts of computational resources. This is where Bayesian Optimization comes in, offering a smarter and more efficient way to optimize hyperparameters.

In this blog, we will dive into the intuition behind Bayesian Optimization, explore its application in Hyperparameter Optimization (HPO), and see how it outperforms traditional methods.

The Challenge of Hyperparameter Tuning

http://The Challenge of Hyperparameter Tuning

Before understanding Bayesian Optimization, let’s first explore the importance of hyperparameter tuning. Hyperparameters are the parameters that govern the training process of a model. Unlike model parameters (e.g., weights in a neural network), hyperparameters are set before training starts and directly influence the model’s performance.

For example, in a decision tree, hyperparameters like tree depth, number of estimators, and learning rate can drastically affect the model’s accuracy. Choosing the right combination of these hyperparameters is not trivial, and doing so manually can be time-consuming and computationally expensive.

Traditional methods for hyperparameter tuning include:

1. Manual Search: A user manually adjusts the parameters and evaluates the model performance.
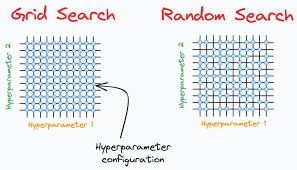
2. Random Search: Hyperparameter values are randomly sampled from a predefined range.
3. Grid Search: A grid is created over the hyperparameter space, and all combinations of hyperparameters are evaluated.

While Random Search and Grid Search can be effective in some cases, they do not consider past evaluations, making them inefficient. Bayesian Optimization, on the other hand, uses past results to intelligently explore the hyperparameter space, leading to faster convergence and more efficient optimization.

What is Bayesian Optimization?

Bayesian Optimization is a global optimization technique that is particularly useful for optimizing black-box functions, like hyperparameter tuning. A black-box function is one where we do not know the underlying function or its gradient, making it difficult to compute the optimal solution using traditional methods. In machine learning, the objective function we want to minimize (or maximize) is the model performance (e.g., accuracy or loss), which depends on the hyperparameters.

Bayesian Optimization works by building a probabilistic model of the objective function and using it to select the most promising hyperparameter configurations to evaluate next. It aims to find the optimal set of hyperparameters with fewer function evaluations than traditional methods.

How Bayesian Optimization Works: A Step-by-Step Intuition

Let’s walk through the process of Bayesian Optimization using the example of optimizing hyperparameters for a Random Forest regression model.

1. Define the Objective Function: The objective function in hyperparameter optimization is usually the model’s performance metric (e.g., Root Mean Squared Error (RMSE) for regression models). We want to minimize RMSE by selecting the best hyperparameters.
2. Surrogate Model: Since the true objective function is unknown, we create a surrogate model that approximates it. This surrogate is a probabilistic model that represents the underlying objective function. The most common model used in Bayesian Optimization is the Gaussian Process (GP), which captures the uncertainty of the objective function.
3. Acquisition Function: Once we have the surrogate model, we use an acquisition function to decide which set of hyperparameters to evaluate next. The acquisition function determines where to sample next in the hyperparameter space, balancing between exploring regions with high uncertainty and exploiting regions known to have good performance.Common acquisition functions include:
   • Expected Improvement (EI)
   • Probability of Improvement (PI)
   • Upper Confidence Bound (UCB)
4. Evaluation and Iteration: After selecting the next set of hyperparameters using the acquisition function, we evaluate the model’s performance with these parameters (i.e., compute the objective function, such as RMSE). This new data point is added to the history of evaluations, which updates the surrogate model. This process repeats iteratively until we converge to the optimal hyperparameter set or reach a predefined number of iterations.

Why Bayesian Optimization is Better than Random Search and Grid Search

• Efficiency: Unlike Grid Search and Random Search, Bayesian Optimization uses previous evaluations to guide future sampling, making it much more efficient in exploring the hyperparameter space.
• Intelligent Exploration: By modeling the objective function probabilistically, Bayesian Optimization can identify the regions of the hyperparameter space that are likely to contain the optimum, leading to faster convergence.
• Less Computationally Expensive: Since fewer evaluations are needed compared to traditional methods, Bayesian Optimization is ideal for expensive black-box functions, such as hyperparameter tuning in deep learning models.

The Sequential Model-Based Optimization (SMBO) Algorithm

Bayesian Optimization is often implemented using the Sequential Model-Based Optimization (SMBO) algorithm. SMBO builds a probabilistic surrogate model of the objective function and uses an acquisition function to decide which hyperparameters to evaluate next. The process is sequential because the algorithm iteratively updates the surrogate model with new evaluations.

Steps in SMBO (Bayesian Optimization) Algorithm

1. Initialize the Surrogate Model with the first set of hyperparameter values.
2. Evaluate the Objective Function at the chosen hyperparameters.
3. Update the Surrogate Model using the new data point.
4. Use the Acquisition Function to select the next set of hyperparameters to evaluate.
5. Repeat until convergence or maximum iterations.

Types of Surrogate Models and Acquisition Functions

1. Gaussian Process (GP): The most common surrogate model, capturing uncertainty in the objective function.
2. Tree of Parzen Estimators (TPE): An alternative model, used in libraries like Hyperopt, that models the probability distribution of hyperparameters given the objective function score.

Expected Improvement (EI) is a popular acquisition function, which balances exploration and exploitation by considering both the predicted mean and variance of the surrogate model.

Conclusion: The Power of Bayesian Optimization in Hyperparameter Tuning

Bayesian Optimization is a powerful tool for hyperparameter optimization, especially when dealing with expensive black-box functions that require significant computational resources. By using a probabilistic model to guide the search for optimal hyperparameters, Bayesian Optimization reduces the number of evaluations needed and accelerates the tuning process.

For machine learning practitioners, adopting Bayesian Optimization can lead to more efficient use of computational resources, quicker convergence to optimal models, and better performance overall.

As you work on complex machine learning projects, consider integrating Bayesian Optimization into your hyperparameter tuning workflow to save time and achieve more precise results.