comprehensive guide to Accelerating Backpropagation with BPPSA: A Parallel Approach to Deep Learning Optimization 2024

Deep learning has made tremendous advancements, powering technologies in computer vision, natural language processing, and autonomous systems. However, as models grow in size and complexity, training these models requires immense computational resources. One of the most computationally intensive parts of the training process is backpropagation (BP), which is used to calculate gradients for model parameters. BP is highly sequential, meaning that the computation of gradients for each layer depends on the gradients of the previous layers, making it difficult to parallelize effectively.

In this blog, we explore the Parallel Scan Algorithm (BPPSA), a novel approach that aims to address the strong sequential dependency of backpropagation and improve the scalability of deep learning models. We will break down how BPPSA works, its advantages over traditional BP, and how it achieves up to 108× speedup in the backward pass of training.

The Problem with Sequential Backpropagation

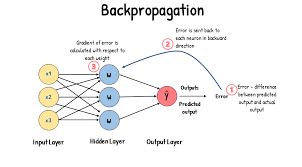
The backpropagation algorithm, introduced by Rumelhart et al. in the 1980s, is the cornerstone of training deep learning models. However, a key limitation of BP is its strong sequential dependency across the layers during gradient computation. Specifically, in a typical neural network, the gradient for each layer needs to be calculated sequentially, which becomes a bottleneck when scaling up training.

For instance, in data parallelism, while multiple GPUs can compute gradients for different batches of data, the sequential nature of BP means that layers must still be processed in order, with each layer depending on the result from the previous one. This sequential bottleneck severely limits the efficiency of parallel systems, particularly when training on larger models or datasets.

The BPPSA Approach

To overcome the limitations of sequential backpropagation, the Backpropagation by Parallel Scan Algorithm (BPPSA) reformulates the BP algorithm as a scan operation, which is a fundamental concept in parallel computing.

The key idea behind BPPSA is to break down the BP computation into a series of binary, associative operations (such as matrix multiplication) that can be performed in parallel, using a technique called the Blelloch scan. This scan operation is a well-known parallel algorithm that computes partial reductions over a sequence of elements efficiently.

By utilizing the scan operation, BPPSA can reduce the complexity of backpropagation from Θ(n) steps (in the traditional method) to Θ(log n) steps, providing a logarithmic speedup on parallel systems. This allows for better utilization of multi-core processors and GPUs, enabling faster training times.

How BPPSA Works

Reformulation of BP as a Scan Operation: The BP algorithm is modified so that the matrix multiplications involved in the gradient calculations become binary and associative. This allows for parallelization using scan operations, which reduces the number of sequential dependencies.
Up-sweep and Down-sweep Phases: BPPSA uses the Blelloch scan algorithm, which consists of two phases:
- Up-sweep Phase: The partial sums are computed in parallel using a reduction tree.
- Down-sweep Phase: The partial sums are combined across branches, and the final result is reconstructed.
Exploiting Sparsity in Jacobians: One of the challenges in backpropagation is the Jacobian matrix—the matrix that computes the gradient for each layer. These Jacobians are often sparse, meaning that many of the elements are zero, and leveraging this sparsity can lead to significant performance improvements. BPPSA exploits this sparsity by generating Jacobians efficiently and reducing memory usage during the training process.

Key Results: Speedup and Efficiency

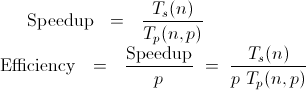
Θ(log n) vs. Θ(n): BPPSA achieves a logarithmic speedup in gradient computations compared to the traditional BP approach. While standard backpropagation takes linear time per step, BPPSA reduces this to logarithmic time, making the process much faster on parallel systems.
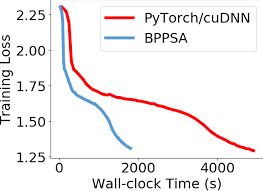
Speedup of up to 108×: In empirical tests, BPPSA demonstrated a backward pass speedup of up to 108× compared to traditional BP methods. This translates to a 2.17× overall speedup in model training, significantly reducing training times for large models.
Memory Efficiency: BPPSA also improves memory efficiency by leveraging sparse Jacobians and reducing the memory requirements of the backward pass. For instance, the first convolution in a VGG-11 model for CIFAR-10 images could occupy 768 MB of memory. BPPSA reduces this by generating the Jacobians more efficiently.

Performance Benefits and Real-World Impact

The performance benefits of BPPSA become even more evident as the model size and the number of workers (GPUs or machines) increase. BPPSA scales efficiently with the model length and the number of parallel workers. This makes it an ideal solution for training large deep learning models on multi-GPU setups, where traditional backpropagation struggles to fully utilize the available hardware.

Sensitivity to Model Length: The method scales well with longer models, and as the sequence length (or model length) increases, the benefits of BPPSA become more pronounced, showing 108× speedup until bounded by the number of workers.
Sensitivity to Number of Workers: BPPSA is also sensitive to the number of workers. As the number of GPUs or devices increases, the efficiency of the method improves, especially when dealing with large models.
GPU Performance: Benchmark tests on GPUs, such as the RTX 2070 and RTX 2080 Ti, demonstrate that BPPSA delivers faster training times, with the RTX 2080 Ti showing improved latency compared to the RTX 2070 due to more streaming multiprocessors.

Conclusion: The Future of Parallel Deep Learning

BPPSA presents a breakthrough in optimizing the backpropagation algorithm by leveraging parallel scan operations to overcome the sequential bottlenecks of traditional BP. The result is a significant speedup in training and reduced memory consumption, which makes BPPSA an attractive solution for large-scale deep learning tasks.

As deep learning models continue to grow in size and complexity, efficient parallelization techniques like BPPSA will be essential in speeding up training times and improving model performance. By reducing training time and leveraging parallelism effectively, BPPSA helps accelerate the development of cutting-edge models, making deep learning more accessible and efficient.

Incorporating BPPSA into your deep learning workflows can lead to more efficient use of computational resources, faster iteration, and ultimately better-performing models—an essential step as we push the boundaries of AI.