comprehensive guide to Arithmetic Intensity for Optimizing Deep Learning Performance 2024
As deep learning models continue to evolve and grow in complexity, performance optimization has become increasingly crucial. Whether it’s image recognition, natural language processing, or autonomous systems, optimizing the computational performance of deep neural networks (DNNs) can significantly reduce training time and resource consumption. A key concept in optimizing performance is arithmetic intensity, a measure that plays a critical role in determining whether an operation is compute-bound or memory-bound.
In this blog, we will explore the concept of arithmetic intensity, how it impacts deep learning performance, and how to use it to optimize training on GPUs.
What is Arithmetic Intensity?
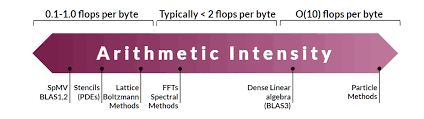
Arithmetic intensity is a metric that helps measure the balance between the amount of computational work and the amount of memory data that needs to be accessed for that computation. It’s a crucial concept when optimizing deep learning models, especially for operations like matrix multiplications, which are at the heart of many deep learning algorithms (e.g., fully-connected layers, convolutional layers, and recurrent layers).
Arithmetic intensity is defined as the ratio of the number of operations (FLOPs) to the amount of data accessed from memory (in bytes). This ratio indicates how efficiently a system utilizes the available memory and computational bandwidth.
Formula for Arithmetic Intensity
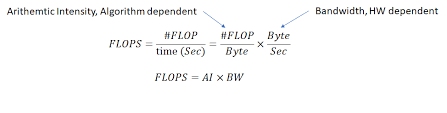
The formula for calculating arithmetic intensity is:Arithmetic Intensity=Number of Operations (FLOPs)Memory Access (Bytes)\text{Arithmetic Intensity} = \frac{\text{Number of Operations (FLOPs)}}{\text{Memory Access (Bytes)}}Arithmetic Intensity=Memory Access (Bytes)Number of Operations (FLOPs)
Where:
- FLOPs represent the number of floating-point operations performed.
- Bytes represent the amount of data accessed from memory.
In simple terms, it measures how many operations are performed per byte of data transferred between the processor and memory. A higher arithmetic intensity indicates that the processor is doing more computation for the same amount of memory access, which can lead to more efficient use of the system’s resources.
How Arithmetic Intensity Affects Performance
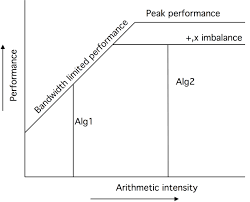
The relationship between memory bandwidth and compute bandwidth determines the performance of an operation. These two factors are influenced by the arithmetic intensity of the algorithm being used. Depending on the relative speeds of memory and compute bandwidth, an operation can be classified as either memory-bound or compute-bound.
Memory-Bound Operations
When the memory bandwidth is the limiting factor, the operation is described as memory-bound. This happens when the amount of data that needs to be loaded from memory exceeds the available computational resources to process it. Common operations like activation functions, pooling, and batch normalization are typically memory-bound because they involve relatively simple computations and frequent memory accesses.
Compute-Bound Operations
On the other hand, compute-bound operations occur when the processor is unable to compute fast enough to keep up with the number of memory accesses. This typically happens when there are complex mathematical operations, such as matrix multiplications or convolution operations, where the computational work (i.e., the number of FLOPs) is much greater than the data transfer. Larger layers of deep learning models tend to have more computations relative to the number of memory accesses, making them compute-bound and suitable for optimization techniques that focus on increasing arithmetic intensity.
How to Measure Arithmetic Intensity
To determine whether an operation is memory-bound or compute-bound, you need to calculate its arithmetic intensity. This can be done using profilers that track both the number of FLOPs and memory access. For example, tools like PyTorch Profiler provide built-in functionality to count the FLOPs and memory accesses for specific modules or operations.
Step-by-Step Process to Calculate Arithmetic Intensity
- Use a Profiler: Start by using a profiler to get the FLOPs count and memory access details. For example, PyTorch’s profiler can be used to calculate FLOPs for each module and operator.
- Track Memory Access: Record the amount of memory accessed by the algorithm. This can be done by monitoring the memory bandwidth during execution.
- Calculate Arithmetic Intensity: Divide the number of operations by the amount of memory accessed. This gives you the arithmetic intensity for the given algorithm and processor.
PyTorch Profiler for Arithmetic Intensity
PyTorch’s profiler has built-in functionality to track the FLOP count and memory access for each operation or module in your model. By using this profiler, you can easily measure arithmetic intensity during training and identify performance bottlenecks in your model.
Optimizing Performance Based on Arithmetic Intensity
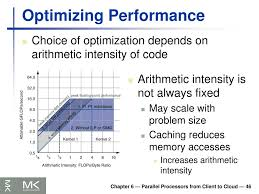
Once you have measured the arithmetic intensity, you can optimize your model depending on whether it is memory-bound or compute-bound:
- Memory-Bound Optimization:
- Optimize Data Access: Reducing memory access and optimizing memory layouts can reduce the memory bandwidth bottleneck. For example, using memory-efficient data types like FP16 (half precision) can decrease the amount of memory required for each operation.
- Reduce Redundant Memory Access: Use techniques like caching to minimize the number of times data is loaded into memory.
- Compute-Bound Optimization:
- Increase Arithmetic Intensity: For compute-bound operations, improving arithmetic intensity by increasing the number of computations (FLOPs) relative to memory accesses can help. One way to achieve this is by optimizing matrix multiplications or using optimized libraries such as cuBLAS for GPU acceleration.
- Parallelization: Leveraging multi-core CPUs or GPUs with specialized tensor cores can increase the number of operations executed in parallel, improving performance for compute-bound tasks.
- Mixed-Precision Training:
- Reduce Precision: Using reduced precision like FP16 instead of FP32 can effectively improve performance without significant loss in accuracy, especially for matrix operations. GPUs like NVIDIA’s Volta architecture with Tensor Cores are optimized for mixed-precision arithmetic, making them ideal for this optimization.
Conclusion: Maximizing Performance with Arithmetic Intensity
Understanding and optimizing arithmetic intensity is a key strategy for improving the performance of deep learning models, particularly when training on GPUs. By measuring arithmetic intensity and understanding whether an operation is memory-bound or compute-bound, you can tailor optimization techniques to better utilize your hardware resources.
Optimizing for compute-bound operations involves increasing the arithmetic intensity through efficient computation and parallelism, while optimizing memory-bound operations focuses on reducing memory access overhead and improving data flow. Tools like PyTorch Profiler and mixed-precision training can assist in these optimization tasks, helping you maximize the efficiency of your deep learning models.
As deep learning continues to push the boundaries of what’s possible, leveraging the concept of arithmetic intensity will remain an essential aspect of building high-performance models that can scale efficiently with growing data and computational complexity.