Understanding SVM: Intuition, Optimization, and Why It’s Effective for Classification Tasks 2024
Support Vector Machines (SVM) are one of the most powerful machine learning algorithms, particularly used for classification and regression tasks. While SVMs are often used in practical applications due to their effectiveness, their underlying concepts and optimization processes might be confusing at first. In this blog, we will break down the intuition behind SVMs, explore their optimization goals, and discuss how they work better than other algorithms like perceptrons.
Motivation Behind SVMs

SVMs were introduced to solve some of the key challenges faced by simpler algorithms like Perceptrons. The primary goal of SVMs is to find a hyperplane that not only separates the data into distinct classes but does so with the maximum margin, ensuring the model generalizes better on new data.
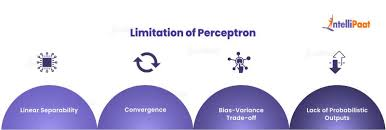
Problems with Perceptrons
Perceptrons were one of the earliest attempts at supervised learning for classification. However, they face several limitations:
- Non-Linearly Separable Data: Perceptrons struggle when the data is not linearly separable. In such cases, finding a linear boundary that divides the data into two distinct classes is impossible.
- Multiple Hyperplanes: Even for linearly separable data, multiple hyperplanes could separate the data, but not all hyperplanes would be equally effective.
- Overfitting: Perceptrons tend to stop once they achieve zero errors on the training data. However, this may not always yield the best boundary, leading to overfitting.
SVM: The Solution to Perceptron Limitations
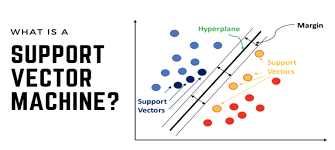
SVMs were developed to address these issues. An SVM classifier works by finding the optimal hyperplane that maximizes the margin between two classes, making it less sensitive to overfitting. The margin is the distance between the hyperplane and the closest data points from either class (the support vectors). The larger the margin, the better the model’s generalization on unseen data.
Key Concepts of SVMs:
- Support Vectors: These are the data points closest to the decision boundary. They are critical in defining the margin and the decision hyperplane.
- Maximizing the Margin: SVMs aim to maximize the distance between the support vectors and the hyperplane, improving model robustness.
How Does SVM Optimization Work?
The optimization objective in SVM is quite simple but powerful. We need to find a hyperplane that maximizes the margin between the two classes. Mathematically, we want to maximize γ\gammaγ (the margin) by varying the weight vector www and the bias bbb, subject to certain constraints.
For each data point (xi,yi)(x_i, y_i)(xi,yi) in the dataset, the following constraint must hold:
- For points of class yi=+1y_i = +1yi=+1, the equation w⋅xi+b≥γw \cdot x_i + b \geq \gammaw⋅xi+b≥γ holds.
- For points of class yi=−1y_i = -1yi=−1, the equation w⋅xi+b≤−γw \cdot x_i + b \leq -\gammaw⋅xi+b≤−γ holds.
This essentially forces the model to place a gap (margin) of size γ\gammaγ between the two classes.
Formulating the SVM Objective:
The SVM optimization problem can be formally stated as:
- Objective: Maximize γ\gammaγ by varying www and bbb.
- Constraints: For all iii, the condition yi(w⋅xi+b)≥γy_i (w \cdot x_i + b) \geq \gammayi(w⋅xi+b)≥γ must hold.
In essence, SVM tries to find the optimal hyperplane by balancing between minimizing classification errors and maximizing the margin.
Intuition Behind Maximizing the Margin
Maximizing the margin is an important concept because:
- Larger Margin = Better Generalization: A larger margin ensures that the model is not overly sensitive to small variations in the data, thus reducing the risk of overfitting.
- Support Vectors Define the Model: Interestingly, only the support vectors (the closest data points to the hyperplane) influence the model. This means that SVMs are more memory-efficient and focus on the most informative data points.
Visualizing the Optimization Process
Imagine a 2D scenario where data points from two classes are plotted. The SVM algorithm will look for a line (or hyperplane in higher dimensions) that divides these two classes while maximizing the distance between the nearest points (support vectors) from each class.
In this scenario:
- The blue line represents the decision boundary (hyperplane).
- The dashed lines on either side represent the margins.
- The support vectors are the data points closest to the margin.
This graphical approach makes it clear that SVM chooses the best boundary by ensuring that the margin is as large as possible, leading to better predictions on unseen data.
Soft Margin SVM
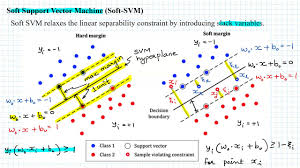
While SVM is effective for linearly separable data, real-world data is often noisy, and perfect separation is not always possible. This is where the soft margin SVM comes into play.
Soft margin SVM introduces a penalty for misclassifications (through slack variables) and tries to balance between maximizing the margin and minimizing classification errors. This allows SVM to handle non-linearly separable data, making it more robust in practice.
Using Kernels for Non-Linearly Separable Data
When data is not linearly separable in its original space, SVMs can use a technique called the kernel trick. The kernel function maps the input data into a higher-dimensional space, where it is more likely to be linearly separable. The beauty of the kernel trick is that it allows us to compute the inner product between the data points in the higher-dimensional space without explicitly transforming the data, making the computation much more efficient.
Conclusion: The Power of SVM for Classification
SVMs have become one of the most widely used machine learning algorithms due to their ability to perform well on both small and large datasets. By focusing on maximizing the margin, SVMs not only ensure good separation between classes but also enhance the model’s generalization capabilities.
Through optimization techniques such as kernel methods, soft margins, and gradient descent, SVMs can tackle complex real-world classification problems, including non-linearly separable data and noisy datasets. Their ability to find the optimal decision boundary, even in high-dimensional spaces, makes SVMs a go-to choice for many classification tasks in machine learning.