Understanding the Role of Discount Factor (γ) and the Use of Deep Neural Networks in Reinforcement Learning

Introduction to Reinforcement Learning
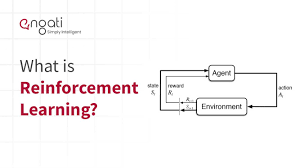
Reinforcement Learning (RL) is a fascinating field of machine learning where an agent learns to make decisions by interacting with an environment. The agent receives feedback in the form of rewards or penalties, allowing it to refine its behavior over time. Two pivotal elements in this learning process are the discount factor (γ) and the application of deep neural networks. In this comprehensive guide, we’ll delve into the significance of the discount factor, explore how it affects agent behavior, and discuss the advantages of integrating deep neural networks into RL systems.
1. The Role of the Discount Factor (γ) in Reinforcement Learning
The discount factor (γ) is a hyperparameter in RL that dictates how much importance the agent gives to future rewards relative to immediate ones. Its value ranges between 0 and 1, serving as a tool to balance short-term gains against long-term benefits.
Understanding the Discount Factor:
When an agent takes an action, it receives a reward. However, the value of this reward isn’t just immediate; it can have implications for future decisions. The discount factor γ helps to calculate the cumulative reward over time, which the agent aims to maximize.
Mathematical Representation:
The total expected reward (also known as the return) starting from a time step tt is given by:
G_t = R_t + γR_{t+1} + γ^2R_{t+2} + ... + γ^kR_{t+k}
Here:
- GtG_t: Total discounted reward starting from time step tt.
- RtR_t: Immediate reward received at time tt.
- γγ: Discount factor.
The factor γkγ^k means that the reward kk steps into the future is discounted exponentially, which reduces its present value.
How γ Affects Agent Behavior:
- γ = 0 (Short-sighted Agent):
- The agent values only immediate rewards and completely ignores future consequences.
- This leads to policies that focus on short-term gains, potentially sacrificing long-term success for quick rewards.
- Example: In a game, an agent might take a risky move to get a small immediate reward, even if it jeopardizes future success.
- 0 < γ < 1 (Balanced Agent):
- The agent values future rewards but discounts them progressively as they move further into the future.
- A higher γ (close to 1) makes the agent more future-oriented, whereas a lower γ (closer to 0) focuses the agent on nearer rewards.
- Example: With γ = 0.9, the agent would consider rewards from future steps significantly, making decisions that are beneficial in the long run.
- γ close to 1 (Far-sighted Agent):
- The agent treats future rewards almost equally to immediate ones, leading to strategies that prioritize long-term gains.
- This is useful in scenarios where planning several steps ahead is crucial.
- Example: In chess, a high γ would encourage the agent to make moves that ensure long-term control of the board rather than capturing a piece immediately.
Choosing the Right γ:
The choice of γ depends on the problem at hand:
- Short-Term Tasks: Lower γ values may be appropriate where immediate rewards are more important (e.g., high-frequency trading).
- Long-Term Tasks: Higher γ values are beneficial for tasks that require extensive future planning (e.g., strategic games or robotic navigation).
Code Example for Cumulative Reward Calculation:
<pre>
<code>
# Python example to calculate cumulative reward with discount factor
rewards = [5, 10, 20, 50] # Sequence of rewards over 4 time steps
gamma = 0.8 # Discount factor
# Calculate cumulative discounted reward
cumulative_reward = sum(gamma**i * rewards[i] for i in range(len(rewards)))
print("Cumulative Discounted Reward:", cumulative_reward)
</code>
</pre>
Impact on Learning Speed and Stability:
- A higher γ can slow down learning since the agent must consider the implications of current actions on a more extended sequence of future rewards.
- A lower γ can speed up learning but may lead to suboptimal policies by over-prioritizing immediate rewards.
2. Advantages of Deep Neural Networks in Reinforcement Learning
Deep Reinforcement Learning (Deep RL) merges RL with deep learning, using deep neural networks (DNNs) to approximate complex functions like policies and value functions. This combination has transformed RL, enabling agents to tackle high-dimensional and complex problems effectively.
Key Advantages of Using Deep Neural Networks:
- Scalability to High-Dimensional Inputs:
- DNNs can process complex, high-dimensional data such as images, audio, or sensor data. This allows RL agents to operate in environments where the state space is enormous and not easily handled by traditional methods.
- Example: Playing Atari games from raw pixels or controlling robots using camera inputs.
- Automatic Feature Extraction:
- In traditional RL, manual feature engineering is often required to represent the state adequately. DNNs automate this process by learning relevant features directly from the raw input data during training.
- Example: In image-based tasks, convolutional neural networks (CNNs) can learn features like edges, shapes, and textures crucial for decision-making.
- Function Approximation:
- DNNs can approximate complex functions, making them ideal for modeling value functions (e.g., Q-values) or policies in RL.
- This capability is essential for handling continuous action spaces and large state spaces where tabular methods are infeasible.
- Generalization:
- Neural networks can generalize well to unseen states by leveraging patterns learned during training. This allows RL agents to make reasonable decisions even in situations not encountered during learning.
- Example: A robotic arm trained to pick up objects can adapt to slightly different object shapes and sizes.
- Handling Continuous Action and State Spaces:
- DNNs facilitate RL algorithms like Deep Deterministic Policy Gradient (DDPG) and Actor-Critic methods, which can efficiently work with continuous action spaces.
- Example: Autonomous vehicle steering and acceleration, where actions are continuous values.
- End-to-End Learning:
- Deep RL allows for end-to-end learning, where raw inputs are mapped directly to actions, reducing the need for intermediate processing or feature extraction steps.
- This simplifies the design of RL systems and makes them more versatile across different tasks.
Deep Q-Learning: A Case Study
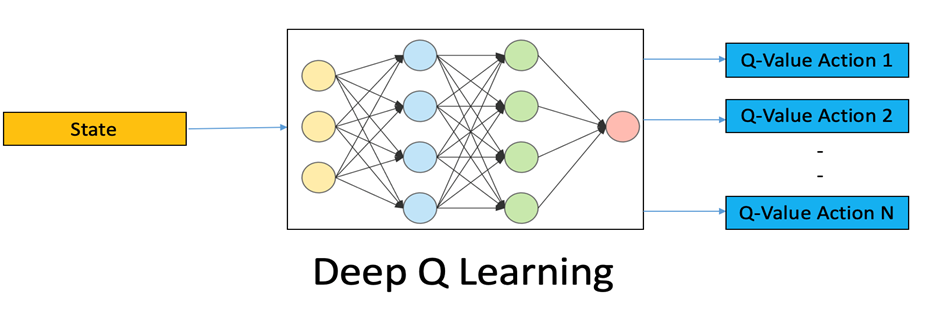
Deep Q-Learning (DQN) is a popular Deep RL algorithm where a deep neural network is used to approximate the Q-value function. The Q-value represents the expected return of taking a specific action in a given state.
Q-Value Update Formula with Neural Network:
Q(s, a) ← R + γ * max_a' Q(s', a')
- Q(s,a)Q(s, a): Current state-action value.
- RR: Immediate reward received after taking action aa in state ss.
- s′s’: Next state resulting from action aa.
- γγ: Discount factor.
Python Code Example for Deep Q-Learning:
<pre>
<code>
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# Build a simple neural network for Q-value approximation
model = Sequential([
Dense(32, input_dim=4, activation='relu'), # Input layer for state space
Dense(32, activation='relu'), # Hidden layer
Dense(2, activation='linear') # Output layer for action space
])
model.compile(optimizer='adam', loss='mse')
# Sample data for Q-value update
state = np.array([0.2, 0.4, 0.6, 0.8]) # Current state
next_state = np.array([0.3, 0.5, 0.7, 0.9]) # Next state
reward = 1
gamma = 0.95
# Predict Q-values for current and next state
q_values = model.predict(state.reshape(1, -1))
q_next = model.predict(next_state.reshape(1, -1))
# Update Q-value for chosen action (e.g., action=0)
action = 0
q_values[0][action] = reward + gamma * np.max(q_next)
# Train the model with the updated Q-values
model.fit(state.reshape(1, -1), q_values, verbose=0)
</code>
</pre>
Challenges and Considerations
While Deep RL offers numerous advantages, it also comes with challenges:
- Training Stability: DNNs can be unstable during training, leading to issues like non-convergence or divergence in Q-values.
- Sample Efficiency: Deep RL often requires a large amount of data (experience) to train effectively, making it computationally intensive.
- Exploration vs. Exploitation: Balancing exploration (trying new actions) and exploitation (choosing the best-known action) becomes more complex with high-dimensional action and state spaces.
Conclusion
The discount factor (γ) and deep neural networks are cornerstones of modern reinforcement learning. The discount factor shapes an agent’s outlook on future rewards, striking a balance between short-term and long-term planning. Meanwhile, deep neural networks unlock the potential of RL to solve complex, real-world problems by enabling scalability, automatic feature extraction, and effective decision-making in high-dimensional spaces.
By understanding and leveraging these concepts, you can design intelligent RL systems capable of tackling a wide array of challenges, from playing video games to automating complex industrial processes. Start experimenting with these techniques today, and witness their transformative power in action!