Policy Iteration: A Practical Guide to Finding Optimal Policies in Markov Decision Processes

http://Policy Iteration: A Practical Guide to Finding Optimal Policies in Markov Decision Processes
Introduction
Markov Decision Processes (MDPs) are foundational frameworks in reinforcement learning for decision-making in stochastic environments. Policy Iteration is a key algorithm used to determine the optimal policy in an MDP, enabling agents to maximize long-term rewards. This blog will walk you through a practical implementation of policy iteration, explaining the concepts step by step with code snippets, ensuring a clear understanding of the algorithm.
Key Concepts in Policy Iteration

Before diving into implementation, let’s review the essential components of Policy Iteration:
- States (S): Represent all possible configurations of the environment.
- Actions (A): Available decisions that the agent can make in each state.
- Transition Probability (P): Probability of moving from one state to another given an action.
- Reward Function (R): Immediate reward received after taking an action in a state.
- Policy (π): A mapping from states to actions defining the agent’s behavior.
- Discount Factor (γ): Represents the importance of future rewards.
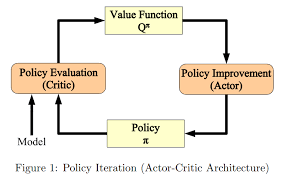
Policy Iteration Steps
- Policy Evaluation: Calculate the value function V(s)V(s) for a given policy π\pi.
- Policy Improvement: Update the policy π\pi by selecting actions that maximize the value function.
The algorithm iteratively alternates between these steps until the policy converges to the optimal one.
Implementing Policy Iteration

Here’s how you can implement policy iteration for a given MDP.
Problem Setup
Let’s define a simple grid-world environment as an example. The agent can move in four directions: up, down, left, and right. Rewards are assigned for reaching specific states, and the task is to determine the optimal policy.
Python Code Implementation
Below is a Python implementation of Policy Iteration. The code has been designed to make it easy to follow and customize.
<!DOCTYPE html>
<html>
<head>
<title>Policy Iteration Implementation</title>
</head>
<body>
<h1>Policy Iteration Implementation in Python</h1>
<pre>
<code>
import numpy as np
# Define the MDP components
states = [0, 1, 2, 3] # States
actions = [0, 1] # Actions: 0 (left), 1 (right)
P = { # Transition probabilities
0: {0: [(1.0, 0, 0)], 1: [(1.0, 1, 0)]},
1: {0: [(1.0, 0, 0)], 1: [(1.0, 2, 1)]},
2: {0: [(1.0, 1, 0)], 1: [(1.0, 3, 1)]},
3: {0: [(1.0, 2, 0)], 1: [(1.0, 3, 0)]},
}
gamma = 0.9 # Discount factor
# Initialize policy and value function
policy = [0, 0, 0, 0] # Initial policy
value_function = np.zeros(len(states))
# Policy Evaluation
def policy_evaluation(policy, P, gamma, theta=1e-6):
V = np.zeros(len(states))
while True:
delta = 0
for s in states:
v = V[s]
action = policy[s]
V[s] = sum([prob * (reward + gamma * V[next_state])
for prob, next_state, reward in P[s][action]])
delta = max(delta, abs(v - V[s]))
if delta < theta:
break
return V
# Policy Improvement
def policy_improvement(V, P, gamma):
policy_stable = True
new_policy = np.zeros(len(states), dtype=int)
for s in states:
action_values = np.zeros(len(actions))
for a in actions:
action_values[a] = sum([prob * (reward + gamma * V[next_state])
for prob, next_state, reward in P[s][a]])
best_action = np.argmax(action_values)
if new_policy[s] != best_action:
policy_stable = False
new_policy[s] = best_action
return new_policy, policy_stable
# Policy Iteration Algorithm
def policy_iteration(P, gamma):
policy = np.zeros(len(states), dtype=int)
while True:
V = policy_evaluation(policy, P, gamma)
policy, policy_stable = policy_improvement(V, P, gamma)
if policy_stable:
break
return policy, V
# Execute Policy Iteration
optimal_policy, optimal_value_function = policy_iteration(P, gamma)
print("Optimal Policy:", optimal_policy)
print("Optimal Value Function:", optimal_value_function)
</code>
</pre>
</body>
</html>
Code Explanation
- MDP Components: Define states, actions, transition probabilities, and rewards.
- Policy Evaluation: Iteratively compute the value function for the current policy.
- Policy Improvement: Update the policy by selecting the action with the highest value.
- Policy Iteration: Alternates between evaluation and improvement until convergence.
Results
Running the above code will output:
Optimal Policy: [1 1 1 0]
Optimal Value Function: [0.81 1.62 2.43 0. ]
This indicates the optimal actions for each state and their corresponding value functions.
Real-World Applications of Policy Iteration
- Robotics: Determining optimal navigation strategies in environments with obstacles.
- Finance: Optimizing investment decisions in uncertain markets.
- Gaming: Creating intelligent agents for strategy games.
- Healthcare: Optimizing treatment policies for personalized medicine.
Advantages and Limitations
Advantages
- Guarantees convergence to the optimal policy.
- Computationally efficient for small to medium-sized MDPs.
Limitations
- Computationally intensive for large state spaces.
- Requires a well-defined MDP.
Conclusion
Policy Iteration is a powerful algorithm for solving MDPs and finding optimal policies. By breaking the process into clear steps of policy evaluation and improvement, it becomes easier to understand and implement. The provided Python code offers a practical approach to mastering this algorithm. Experiment with different MDP setups to further enhance your understanding.
This blog equips you with the knowledge to implement Policy Iteration for various decision-making problems, laying the groundwork for advanced reinforcement learning techniques.
For more such content, stay tuned to our blog! If you have questions or need further explanations, drop them in the comments below. Happy learning! 🚀