The comprehensive guide to Power of Multi-Layer Perceptrons (MLPs) in Deep Learning 2024
Introduction
Multi-Layer Perceptrons (MLPs) are a fundamental part of Deep Neural Networks (DNNs). They are universal approximators capable of solving classification, regression, and Boolean function problems.
🚀 Why Are MLPs Important?
✔ They classify complex decision boundaries.
✔ They can model Boolean functions like XOR gates.
✔ They work for continuous-valued regression tasks.
✔ They are foundational to modern deep learning.
This guide covers:
✅ How MLPs work
✅ How they solve Boolean functions
✅ How many layers are required for complex problems
1. What is a Multi-Layer Perceptron (MLP)?
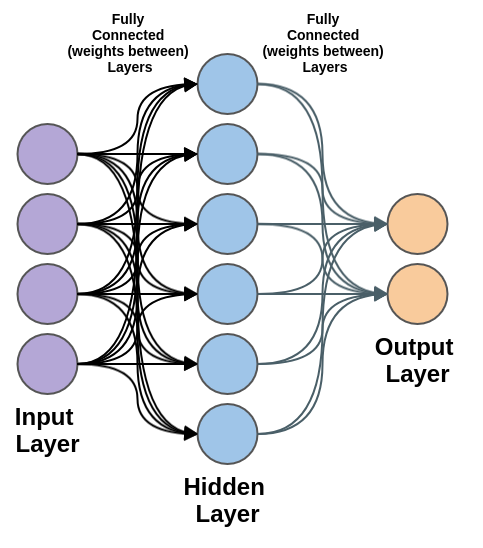
An MLP is a type of artificial neural network composed of multiple layers of perceptrons (neurons). These layers help in learning complex patterns that a single-layer perceptron cannot handle.
🔹 Key Components of an MLP:
✔ Input Layer: Receives raw data (e.g., pixel values in images).
✔ Hidden Layers: Transform data into higher-level features.
✔ Output Layer: Produces final predictions (classification or regression).
🚀 Example:
An MLP trained on handwritten digits (0-9) can classify images based on pixel intensity.
✅ Why Use MLPs?
✔ They learn hierarchical representations of data.
✔ They work for binary, multi-class classification & regression.
✔ They model non-linearly separable functions (e.g., XOR gates).
2. MLPs for Boolean Functions: The XOR Problem

A single-layer perceptron cannot model XOR functions due to their non-linearity. However, an MLP with at least one hidden layer can represent XOR.
🔹 Why can’t a perceptron model XOR?
✔ XOR is not linearly separable (cannot be separated by a straight line).
✔ A single perceptron can only handle linearly separable problems.
✔ Solution: Use two hidden nodes to transform the input space.
🚀 Example: XOR using an MLP 1️⃣ First hidden layer transforms input into linearly separable features.
2️⃣ Second layer combines these features to compute XOR output.
✅ Result:
A two-layer MLP can solve XOR, proving its power over single-layer perceptrons.
3. MLPs for Complicated Decision Boundaries
MLPs can learn complex decision boundaries that single-layer perceptrons cannot.
🔹 Example:
Consider a classification problem where data points cannot be separated by a straight line.
✔ A single-layer perceptron fails because it only models linear decision boundaries.
✔ An MLP learns curved boundaries using multiple hidden layers.
✔ Each layer extracts higher-level patterns, making MLPs powerful classifiers.
✅ Key Takeaway:
The deeper the MLP, the more complex patterns it can learn.
4. How Many Layers Are Needed for a Boolean MLP?
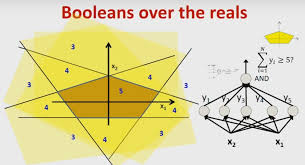
The number of hidden layers in an MLP depends on problem complexity.
| MLP Depth | Use Case |
|---|---|
| 1 Hidden Layer | Solves XOR and simple decision boundaries |
| 2-3 Hidden Layers | Captures complex patterns in images, text, and speech |
| Deep MLP (4+ Layers) | Handles highly intricate patterns (e.g., deep learning for NLP) |
🚀 Example: Boolean MLP
✔ A Boolean MLP represents logical functions over multiple variables.
✔ For functions like W ⊕ X ⊕ Y ⊕ Z, we need multiple perceptrons to combine XOR operations.
✅ Rule of Thumb:
✔ Shallow networks work well for simple problems.
✔ Deeper networks capture hierarchical patterns.
5. Reducing Boolean Functions Using MLPs
MLPs can also reduce Boolean functions using efficient representations.
✔ They minimize the number of neurons required to compute Boolean expressions.
✔ They help simplify complex logic gates using fewer layers.
🚀 Example:
If an MLP represents a complex Boolean function, it can: ✔ Reduce the number of perceptrons needed.
✔ Optimize network depth while maintaining accuracy.
✅ Key Takeaway:
MLPs simplify logical computations, making them more efficient.
6. MLP for Regression: Predicting Continuous Values
Beyond classification, MLPs can handle regression tasks, where the output is a real number.
🔹 Example: Predicting House Prices
✔ Inputs: Square footage, number of bedrooms, location.
✔ Hidden Layers: Extract patterns (e.g., price trends based on location).
✔ Output Layer: Predicts house price as a continuous value.
✅ Key Insight:
MLPs can model complex, non-linear relationships in data.
7. MLPs for Arbitrary Classification Boundaries
MLPs can handle any dataset with enough neurons.
🔹 Example: Recognizing Faces
✔ An MLP trained on facial features learns to classify:
- Different emotions (Happy, Sad, Neutral).
- Different individuals.
🚀 Why are MLPs used in AI?
✔ Handle structured & unstructured data.
✔ Recognize complex relationships.
✔ Adapt to new data over time.
✅ Conclusion:
MLPs are versatile, universal approximators used in AI, deep learning, and decision-making.
8. Key Takeaways
✔ MLPs are multi-layer networks that learn complex patterns.
✔ They solve classification, regression, and Boolean logic problems.
✔ MLPs require backpropagation for weight updates.
✔ More layers = better decision boundaries, but risk of overfitting.
✔ MLPs are foundational to modern AI and deep learning.
💡 How are you using MLPs in your projects? Let’s discuss in the comments! 🚀
Would you like a hands-on Python tutorial for building an MLP with TensorFlow? 😊