Understanding comprehensive guide Multi-Layer Perceptrons (MLPs) in Deep Neural Networks 2024

Introduction

Multi-Layer Perceptrons (MLPs) are a foundational architecture in deep learning. They serve as the backbone for many classification, regression, and universal approximation tasks. By stacking multiple perceptron layers, MLPs can model complex decision boundaries that simple perceptrons cannot.

🚀 Why Learn About MLPs?

✔ Can solve classification (binary & multiclass) and regression problems
✔ Acts as a universal function approximator
✔ Can model arbitrary decision boundaries
✔ Represents Boolean functions for logic-based tasks

In this guide, we will cover:
✅ How MLPs work
✅ MLPs for Boolean functions (XOR gate example)
✅ Number of layers needed for complex classification
✅ How MLPs handle arbitrary decision boundaries

1. What is a Multi-Layer Perceptron (MLP)?

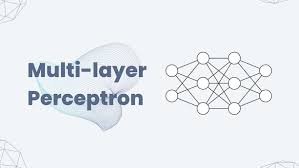
An MLP is a feedforward neural network composed of multiple layers of perceptrons. It includes:
✔ Input layer – Receives raw features
✔ Hidden layers – Extract patterns and transform data
✔ Output layer – Produces the final prediction

🔹 Key Features of MLPs:
✔ Fully connected layers – Every neuron in one layer connects to every neuron in the next layer
✔ Uses activation functions (ReLU, Sigmoid, etc.) to introduce non-linearity
✔ Trained using backpropagation and gradient descent

✅ Why MLPs?
MLPs are called Universal Approximators, meaning they can represent any continuous function, given enough neurons and layers.

2. MLPs for Boolean Functions: XOR Example

A single-layer perceptron cannot model XOR functions due to their non-linearity. However, an MLP with at least one hidden layer can represent XOR.

🔹 Why can’t a perceptron model XOR?
✔ XOR is not linearly separable (i.e., it cannot be separated by a straight line).
✔ A single perceptron can only handle linearly separable problems.
✔ Solution: Use two hidden nodes to transform the input space.

🚀 Example: XOR using MLP 1️⃣ First hidden layer transforms input into linearly separable features
2️⃣ Second layer combines these features to compute XOR output

✅ Result: A two-layer MLP can solve XOR, proving its power over single-layer perceptrons.

3. MLPs for Complex Decision Boundaries

MLPs are widely used because they can represent complicated decision boundaries.

🔹 Example:
Consider a classification problem where data points cannot be separated by a straight line (e.g., spiral datasets).

✔ A single-layer perceptron fails because it can only model linear boundaries.
✔ An MLP can learn complex, curved boundaries using multiple hidden layers.
✔ Each layer extracts higher-level patterns, making MLPs powerful classifiers.

✅ Takeaway:
The deeper the MLP, the more complex patterns it can learn.

4. How Many Layers Do You Need?

The number of hidden layers in an MLP depends on problem complexity.

MLP Depth	Use Case
1 Hidden Layer	Solves XOR and simple decision boundaries
2-3 Hidden Layers	Captures complex patterns in images, text, and speech
Deep MLP (4+ Layers)	Handles highly intricate patterns (e.g., deep learning for NLP)

🚀 Example: Boolean MLP
✔ A Boolean MLP represents logical functions over multiple variables.
✔ For functions like W ⊕ X ⊕ Y ⊕ Z, we need multiple perceptrons to combine XOR operations.

✅ Rule of Thumb:
✔ Shallow networks work well for simple problems.
✔ Deeper networks capture hierarchical patterns.

5. Training MLPs: Backpropagation

MLPs learn through backpropagation, an optimization technique that:
✔ Calculates errors in predictions
✔ Updates weights using gradient descent
✔ Repeats until the model converges

📌 Mathematical Representation:
If Z = W * X + b is the weighted sum, the neuron applies an activation function f(Z):A=f(W∗X+b)A = f(W * X + b) A=f(W∗X+b)

✅ Why Backpropagation?
✔ Ensures that the model learns from mistakes
✔ Uses gradient descent to minimize error over time

🚀 Example: Classifying Handwritten Digits
✔ An MLP processes image pixel values as inputs.
✔ It learns to differentiate digits (0-9) over multiple iterations.
✔ The network adjusts weights after each training step for better accuracy.

6. MLP for Regression: Predicting Continuous Values

Beyond classification, MLPs can also handle regression tasks, where the output is a real number.

🔹 Example: Predicting House Prices
✔ Inputs: Square footage, number of bedrooms, location
✔ Hidden Layers: Extract patterns (e.g., price trends based on location)
✔ Output Layer: Predicts house price as a continuous value

✅ Key Insight:
MLPs can model complex, non-linear relationships in data.

7. MLPs for Arbitrary Decision Boundaries

MLPs are universal classifiers capable of handling any dataset with enough neurons.

🔹 Example: Recognizing Faces
✔ An MLP trained on facial features learns to classify:

Different emotions (Happy, Sad, Neutral)
Different individuals

🚀 Why are MLPs used in AI?
✔ Handle structured & unstructured data
✔ Recognize complex relationships
✔ Adapt to new data over time

✅ Conclusion: MLPs are versatile, universal approximators used in AI, deep learning, and decision-making.

8. Key Takeaways

✔ MLPs are multi-layer networks that learn complex patterns.
✔ They solve classification, regression, and Boolean logic problems.
✔ MLPs require backpropagation for weight updates.
✔ More layers = better decision boundaries, but risk of overfitting.
✔ MLPs are foundational to modern AI and deep learning.

💡 How are you using MLPs in your projects? Let’s discuss in the comments! 🚀

Would you like a hands-on Python tutorial for building an MLP with TensorFlow? 😊